Policy Optimization

1. Introduction

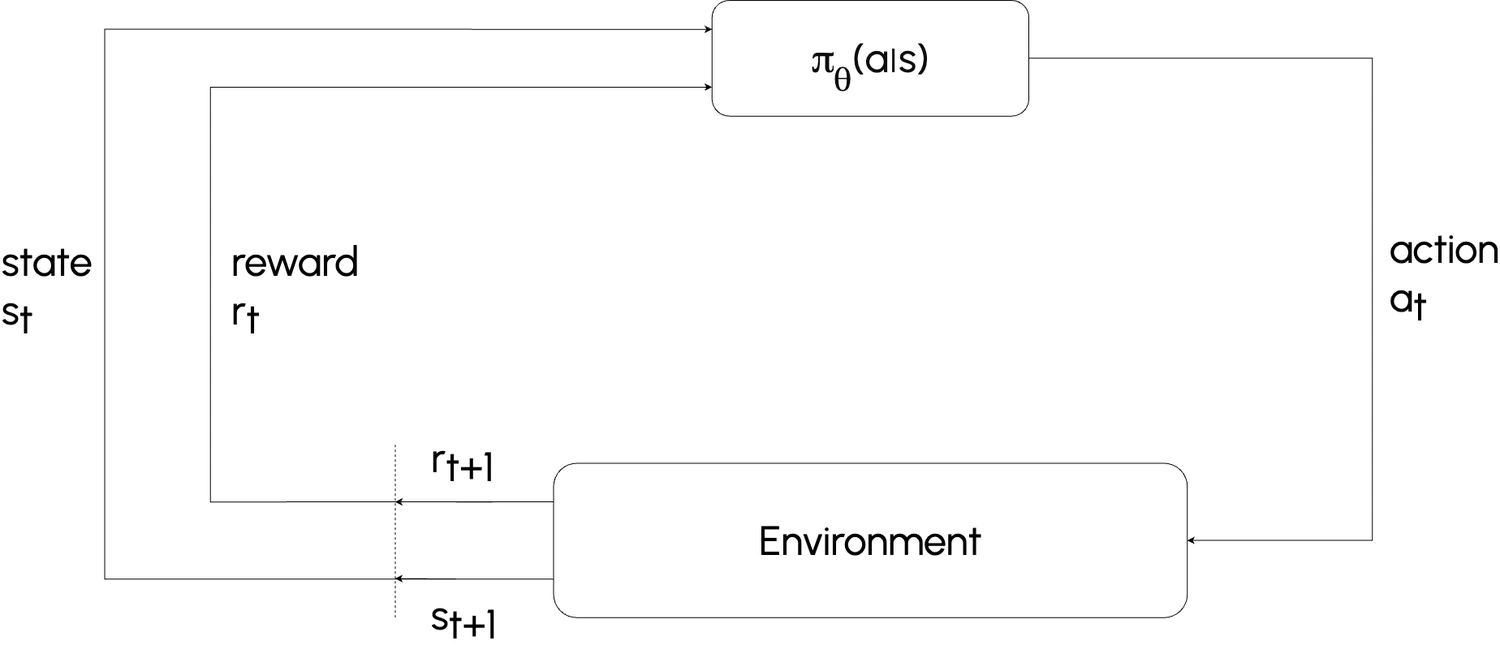
In reinforcement learning, an agent interacts with an environment by taking actions, which lead to new situations. This process repeats continuously. In policy gradient methods, the agent uses a policy (denoted as π_θ) to select actions based on the current state or observation (e.g., an image or a vector).

The policy π_θ(a∣s) represents the probability of taking action a given state s, and it is parameterized by θ, which are the weights of the neural network representing the policy. The goal is to adjust these parameters to maximize the expected cumulative reward:

$$
 \max_{\theta} \; \mathbb{E}_{\pi_\theta} \left[ \sum_{t=0}^H R(s_t, a_t) \right]
$$

where:

• R(s_t, a_t) is the reward obtained after taking action a_t in state s_t,
• H is the time horizon of the task,
• π_θ(a∣s) is the probability of selecting a in state s under policy π_θ.

2. Why Use a Stochastic Policy?

1. Smoothing the Optimization:
   Deterministic policies produce sharp decision boundaries, which can make optimization more difficult. By outputting π_θ(a∣s), a probability distribution over actions, stochastic policies allow for smoother transitions between policies, improving optimization in a continuous policy space.

2. Exploration:
   Stochastic policies introduce randomness into action selection, enabling the agent to explore the environment more effectively. This exploration is essential for collecting diverse data and avoiding suboptimal policies caused by premature convergence.

Conclusion: The stochastic policy π_θ(a∣s) enables the agent to balance smooth optimization and effective exploration by outputting a distribution over possible actions given the current state.

3. Why Policy Optimization

Policy optimization is often preferred over learning Q-values or value functions for several compelling reasons:

1. Simplicity:
   Policies can be easier to learn and represent than Q-functions or value functions. For instance, in robotic grasping, directly learning the optimal movement strategy (e.g., closing a gripper) can be simpler and more practical than modeling grasp quality metrics or computing expected rewards.

2. Direct Action Prescriptions:
   Value functions estimate how good a state-action pair is but don't directly suggest which action to take. To derive actions, you would need additional tools, such as a dynamics model, adding unnecessary complexity. Policies directly map states to actions, streamlining decision-making.

3. Computational Efficiency:
   Learning Q-functions involves solving for the best action by finding the arg⁡max⁡_aQ(s,a), which can be computationally expensive, particularly in continuous action spaces. In contrast, policies directly output actions, bypassing this optimization step and enabling faster execution.

4. Compatibility with Stochastic Settings:
   Policies naturally incorporate stochasticity, enabling smoother optimization and better exploration. This is particularly advantageous in environments requiring robust exploration and when a single deterministic policy might not suffice.

4. Summary

Policy optimization methods focus on directly learning a policy π_θ(a∣s) to map states $s$ to actions a. This approach avoids the complexities and inefficiencies associated with learning Q-values or value functions, making it more suitable for tasks with continuous action spaces, complex dynamics, or scenarios requiring exploration.

One of the most powerful and widely used techniques for optimizing policies is Policy Gradient Methods, which we will explore in depth in the next lesson.