1. Introduction
Reinforcement Learning (RL) is a branch of machine learning focused on training agents to make sequences of decisions by interacting with an environment to maximize a cumulative reward. Unlike supervised learning, where agents learn from labeled data, RL agents learn from trial and error, adapting their actions based on feedback from the environment. The agent’s objective is to develop a policy—a strategy for choosing actions in various situations—that leads to the highest possible reward over time. RL has been applied to diverse areas, from video games and robotics to finance and healthcare, for tasks that involve dynamic decision-making and adaptation.
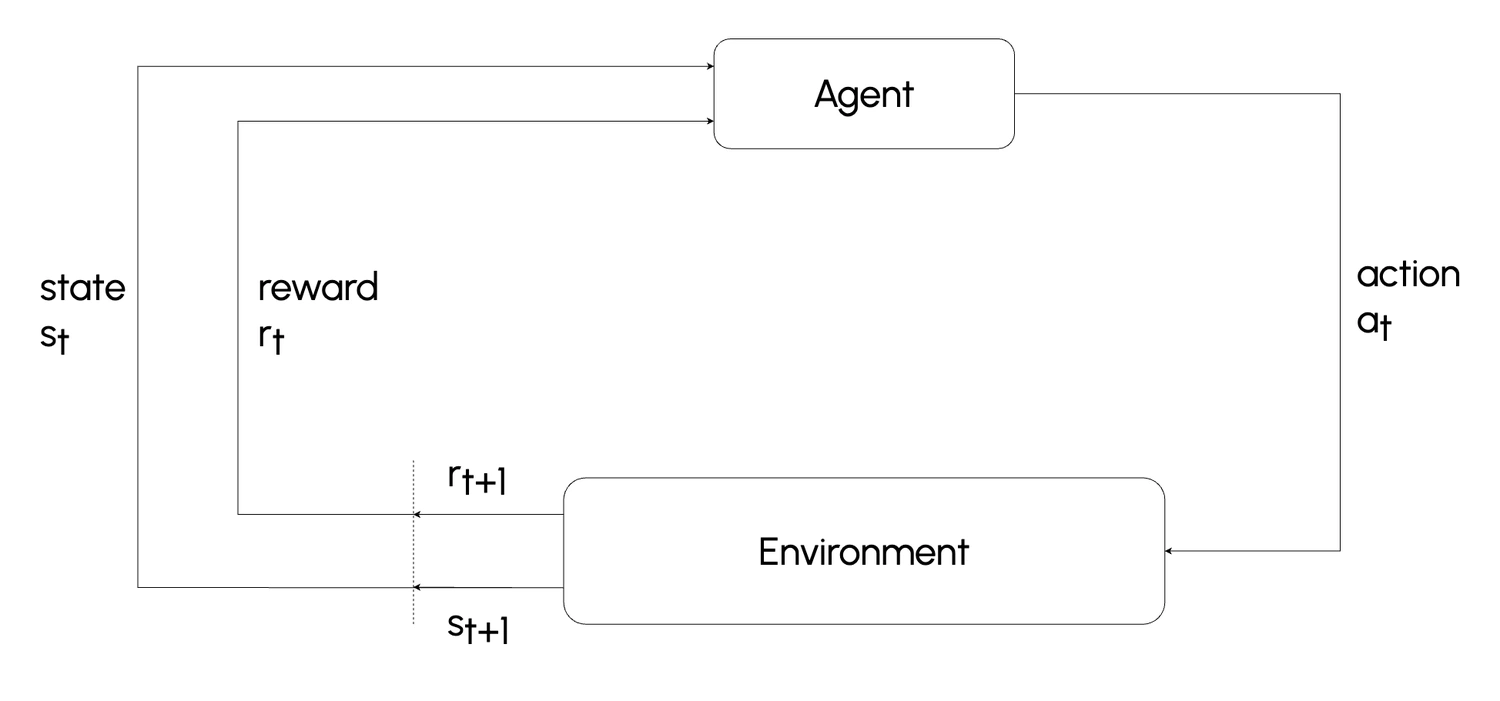
Figure: Reinforcement Learning fundamental diagram
2. Markov Decision Processes
A Markov Decision Process (MDP) is a formal framework for modeling sequential decision-making tasks in reinforcement learning. In an MDP, an agent interacts with an environment through a series of states, actions, and rewards, aiming to learn a policy that maximizes cumulative reward. An MDP is defined by the tuple (S, A, P, R, γ), where:
- Set of States (S): The set of all possible states the agent can occupy.
- Set of Actions (A): The set of all possible actions the agent can take in any given state.
- Transition Function (P(s' | s, a)): A probability function describing the likelihood of transitioning to a next state s' when taking action a in the current state s. Mathematically, this is defined as:
$$ P(s' | s, a) = \Pr(s_t+1 = s' | s_t = s, a_t = a) $$
- Reward Function (R(s, a, s')): A function that assigns a numerical reward for each transition, quantifying the immediate outcome of taking action a in state s and moving to state s'. The reward function can be represented as:
$$ R(s, a, s') = E[r_{t+1} | s_t = s, a_t = a, s_{t+1} = s'] $$
- Discount Factor (γ): A factor γ (between 0 and 1) that determines the importance of future rewards. A lower γ places more emphasis on immediate rewards, while a higher γ favors long-term rewards.
The Markov property asserts that the next state and reward depend only on the current state and action, and not on any past states or actions, which can be expressed as:
$$ Pr(s_{t+1} = s', r_{t+1} = r | s_t, a_t, s_{t-1}, a_{t-1}, … , s_0, a_0) = Pr(s_{t+1} = s', r_{t+1} = r | s_t, a_t) $$
The Horizon defines the number of steps over which the agent seeks to optimize rewards, which may be finite or infinite. A policy π(a|s) describes the probability of choosing action a in state s, and the goal of RL is to learn an optimal policy π* that maximizes the expected cumulative reward over the agent's lifetime.
3. The Goal?
The goal is to maximize the expected discounted sum of rewards accumulated over time. We want to find a policy π that achieves this by maximizing the following expression:
$$ \max_{\pi} \ \mathbb{E}\left[ \sum_{t=0}^{H} \gamma^t \ R(S_t, A_t, S_{t+1}) \ | \ \pi \right] $$
Where:
- H is the horizon, or the maximum time steps over which rewards are considered.
- γ (gamma) is the discount factor that reduces the weight of future rewards.
- E is the expectation over possible outcomes, accounting for the randomness in the environment.
- R(St, At, St+1) is the reward received after transitioning from state St to St+1 by taking action At.
In an MDP (Markov Decision Process), we aim to find an optimal policy π* that defines the best action for each state and time step. Formally, an optimal policy π* can be defined as:
$$ \pi*: S \times \{0:H\} \rightarrow A $$
This means that a policy π provides an action for each state S at each time step from 0 up to horizon H. The goal of the policy is to maximize the expected sum of rewards over time.
In the example grid above, each cell represents a state, and the arrows indicate the actions chosen by the policy for each state. The agent is rewarded with +1 for reaching the goal state (right side) and -1 for entering a penalty state (gray cell). The optimal policy guides the agent to maximize the sum of rewards by moving toward the goal while avoiding penalties.
Contrast: If the environment were deterministic, the agent would only need an optimal plan, or a fixed sequence of actions from start to goal. However, in an uncertain environment, the optimal policy must adapt at each step based on the current state.